最近、Rについてのエントリーが多いことからも察している人も多いと思いますが、最近は仕事でRばっかり使ってます。ある製品群の値段予測システムという社長の案があって、自分はRを用いてその予測価格の算出方法をいろいろ考えているところです。そのデータ自体はデータベースに大量にあるので、それを有効活用しようというわけです。
前々から社長はその案を画策していたそうで、社長から渡された多変量解析の参考書籍には2011年に購入したであろうと思われる栞がはさんでありました。確かあちこちにメモ書きもあったと思うので、社長もよく勉強してるんだと思います。
ところで、解析の対象の項目には、順序があるわけではない、あるカテゴリー変数がありました。隠すことではないのと思うで言ってしまうと、製品の『色』です。ただ、だいたいの人気色というのは予想がつくので、自身でそれぞれの色に数値を割り当てていって精度をあげてほしいということでした。
試しに、下記のニコニコ動画から取得したデータを用いてやってみようと思います。
nico
この場合、ニコ動のカテゴリーがまんまカテゴリー変数ということなります(ややこしいですが)。まずは試しに、再生数とカテゴリーをboxplotで出力してみる。
> nico <- read.table("clipboard", header=T)
> boxplot(view~category, data=nico, ylim=c(0,2000000))
すると、下記のような図となりました(y軸の制限をなくすと縦に長くなりすぎてわかりづらいので、箱が分かる範囲にしています)。
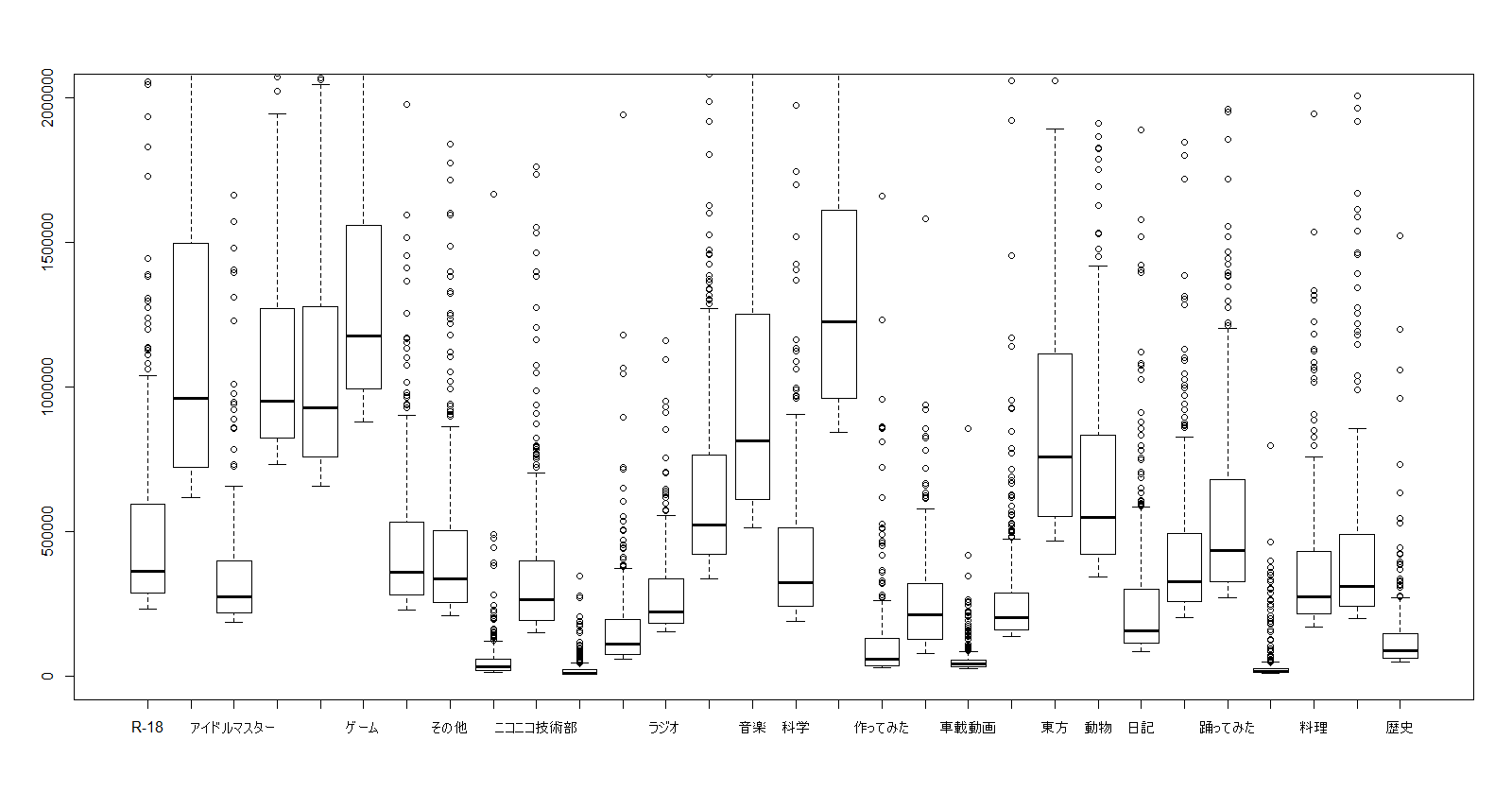
項目名が書いてないところが多いので分かりにくいですが、左から『R-18』『VOCALOID』『アイドルマスター』『アニメ』『エンターテイメント』『ゲーム』『スポーツ』『その他』『ニコニコインディーズ』『ニコニコ技術部』『ニコニコ手芸部』『ニコニコ動画講座』『ラジオ』『演奏してみた』『音楽』『科学』『歌ってみた』『作ってみた』『自然』『車載動画』『政治』『東方』『動物』『日記』『描いてみた』『踊ってみた』『旅行』『料理』『例のアレ』『歴史』 となっています(項目名を縦にして表示したいのですが、調べても分かりませんでした。改行を入れて対処するという方法もあるんですが、図とかぶってしまうので・・・)。
では、これを参考に数値化しています。とりあえず中心点を基準に上のほうにあるものを大きい数値、下の方にあるものを小さい数値であらわしてみます。
とりあえず下記のような感じにしてみました。
> nico$cate_digit <- 0 > nico[nico$category=="R-18",]$cate_digit <- 1 > nico[nico$category=="VOCALOID",]$cate_digit <- 3 > nico[nico$category=="アイドルマスター",]$cate_digit <- 1 > nico[nico$category=="アニメ",]$cate_digit <- 3 > nico[nico$category=="エンターテイメント",]$cate_digit <- 3 > nico[nico$category=="ゲーム",]$cate_digit <- 4 > nico[nico$category=="スポーツ",]$cate_digit <- 1 > nico[nico$category=="その他",]$cate_digit <- 1 > nico[nico$category=="ニコニコインディーズ",]$cate_digit <- 0 > nico[nico$category=="ニコニコ技術部",]$cate_digit <- 1 > nico[nico$category=="ニコニコ手芸部",]$cate_digit <- 0 > nico[nico$category=="ニコニコ動画講座",]$cate_digit <- 0 > nico[nico$category=="ラジオ",]$cate_digit <- 1 > nico[nico$category=="演奏してみた",]$cate_digit <- 2 > nico[nico$category=="音楽",]$cate_digit <- 3 > nico[nico$category=="科学",]$cate_digit <- 1 > nico[nico$category=="歌ってみた",]$cate_digit <- 4 > nico[nico$category=="作ってみた",]$cate_digit <- 0 > nico[nico$category=="自然",]$cate_digit <- 1 > nico[nico$category=="車載動画",]$cate_digit <- 0 > nico[nico$category=="政治",]$cate_digit <- 1 > nico[nico$category=="東方",]$cate_digit <- 3 > nico[nico$category=="動物",]$cate_digit <- 2 > nico[nico$category=="日記",]$cate_digit <- 1 > nico[nico$category=="描いてみた",]$cate_digit <- 2 > nico[nico$category=="踊ってみた",]$cate_digit <- 2 > nico[nico$category=="旅行",]$cate_digit <- 0 > nico[nico$category=="料理",]$cate_digit <- 2 > nico[nico$category=="例のアレ",]$cate_digit <- 2 > nico[nico$category=="歴史",]$cate_digit <- 0
これで重回帰分析できます。試してみましょう。
> nico.lm <- lm(view~comment+mylist+cate_digit, data=nico)
> summary(nico.lm)
Call:
lm(formula = view ~ comment + mylist + cate_digit, data = nico)
Residuals:
Min 1Q Median 3Q Max
-3711339 -121330 -41912 71749 6335034
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.857e+04 6.344e+03 10.81 <2e-16 ***
comment 1.771e-01 9.246e-03 19.15 <2e-16 ***
mylist 2.444e+01 2.401e-01 101.82 <2e-16 ***
cate_digit 1.314e+05 3.869e+03 33.96 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 376200 on 8996 degrees of freedom
Multiple R-squared: 0.7105, Adjusted R-squared: 0.7104
F-statistic: 7358 on 3 and 8996 DF, p-value: < 2.2e-16
決定係数(Multiple R-squared)が0.7105、自由度調整済み決定係数(Adjusted R-squared)が0.7104となっています。悪くなさそうです。もう少し微調整したらもっとよくなるかもしれません。
ところで、その時(一ヶ月ほど前ですが)は自分も統計に関しては全くもって無知で「確かに、数値化しないと計算できないしね。なるほどなるほど」なんて思ってやっていたのですが、いろいろ調べてみるとダミー変数化するという方法があるということを知りました。例えば、黒という変数を用意して、黒い製品には1、他は0。また、白という変数を用意して、白色なら1、ほかは0。という具合に、それぞれのカテゴリーごとに変数を作るというものです。これならわざわざ自分で順序を考えなくてもいいですし、楽ができそうです。
ということを社長に話してみると、こう言われました。
「変数が増えると補正R2が小さくなるからそれはやらないほうがいい」(補正R2とは、自由度調整済み決定係数のこと。Excelではこう記される。初めてExcelで調査してたのでこの言葉が社内では一般的)
なんとも腑に落ちない感じがしたのですが、自分も統計学に関しては初心者だったのでなんとも言えませんでした。
確かに、自由度調整済み決定係数は、決定係数や標本数の数が変わらない状況な場合、変数だけ増えると下がる傾向にあります。
ちなみに、変数の数をp、標本数の数をn、決定係数をR2とすると、自由度調整済み決定係数は下記のようになります。
((n-1)*R2-p)/(n-1-p)
参考:自由度調整済決定係数
上記の重回帰分析の結果を例にもとめてみると、((9000-1)*0.7105-3)/(9000-1-3)となり、確かに結果は0.7104となりました。
ではここで、標本数が20、R2が0.7、変数の数が9と10の場合を考えてみようと思います。
まず、変数の数が9の場合は((20-1)*0.7-10)/(20-1-10)となり、これは0.43になります。10の場合は0.3666666…となりました。確かに変数の数が増えると自由度調整済み決定件数は減るようです(確かあの時社長は、「分母が大きくなるから小さくなる」みたいなことを言っていたような気がするのですが・・・。記憶違いかもしれない。さすがに自分より一年以上も多く統計の勉強をしていた社長がそんな間違いをするとは思えないし)。
なお、上記のニコ動の例をダミー変数化すると下記のような結果に(指数表記をなくしてます)。
> summary(lm(view~comment+mylist+category, data=nico))
Call:
lm(formula = view ~ comment + mylist + category, data = nico)
Residuals:
Min 1Q Median 3Q Max
-3395324 -118156 -20216 55338 5883875
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 458064.530644 19861.043531 23.063 < 0.0000000000000002 ***
comment 0.153421 0.008494 18.063 < 0.0000000000000002 ***
mylist 28.047661 0.246186 113.929 < 0.0000000000000002 ***
categoryVOCALOID -633781.304234 30583.173139 -20.723 < 0.0000000000000002 ***
categoryアイドルマスター -317535.515396 28093.546807 -11.303 < 0.0000000000000002 ***
categoryアニメ -13644.192814 28572.431076 -0.478 0.632996
categoryエンターテイメント 106135.598976 28340.053796 3.745 0.000181 ***
categoryゲーム 413089.540379 28295.190744 14.599 < 0.0000000000000002 ***
categoryスポーツ -134995.033650 28068.815743 -4.809 0.00000153825837490 ***
categoryその他 -202034.584038 28084.684463 -7.194 0.00000000000068089 ***
categoryニコニコインディーズ -462024.040416 28064.173777 -16.463 < 0.0000000000000002 ***
categoryニコニコ技術部 -245200.648811 28064.377112 -8.737 < 0.0000000000000002 ***
categoryニコニコ手芸部 -447217.341148 28070.749371 -15.932 < 0.0000000000000002 ***
categoryニコニコ動画講座 -435513.251157 28064.612221 -15.518 < 0.0000000000000002 ***
categoryラジオ -278794.726266 28062.032450 -9.935 < 0.0000000000000002 ***
category演奏してみた -298862.032598 28305.664227 -10.558 < 0.0000000000000002 ***
category音楽 -252926.867750 29081.489341 -8.697 < 0.0000000000000002 ***
category科学 -138468.120667 28062.210071 -4.934 0.00000081874520230 ***
category歌ってみた -153140.943851 29617.158274 -5.171 0.00000023827385654 ***
category作ってみた -407117.657506 28062.825664 -14.507 < 0.0000000000000002 ***
category自然 -294326.515468 28061.671782 -10.489 < 0.0000000000000002 ***
category車載動画 -415733.907701 28069.852138 -14.811 < 0.0000000000000002 ***
category政治 -257040.944522 28061.635728 -9.160 < 0.0000000000000002 ***
category東方 74088.757120 28395.981210 2.609 0.009092 **
category動物 -55178.640636 28125.047388 -1.962 0.049805 *
category日記 -258370.236222 28061.979800 -9.207 < 0.0000000000000002 ***
category描いてみた -413861.911816 28188.190561 -14.682 < 0.0000000000000002 ***
category踊ってみた -206639.925611 28165.642637 -7.337 0.00000000000023815 ***
category旅行 -432103.331319 28069.900959 -15.394 < 0.0000000000000002 ***
category料理 -225171.789781 28066.504672 -8.023 0.00000000000000116 ***
category例のアレ -198804.347317 28073.685989 -7.082 0.00000000000153320 ***
category歴史 -382580.615734 28063.243009 -13.633 < 0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 343700 on 8968 degrees of freedom
Multiple R-squared: 0.7591, Adjusted R-squared: 0.7583
F-statistic: 911.6 on 31 and 8968 DF, p-value: < 0.00000000000000022
自由度調整済み決定係数が、増えてるという・・・。
さて、例がものすっごい悪かったのですが、実は業務で使っていた解析では数値を調整することにより、自由度調整済み決定係数がダミー変数化する場合より大きくなりました。
ところで、ダミー変数を使うということは変数の値は1か0かということになります。ということは、ダミー変数を使って出てきた係数を使って数値化し、1という数値のほうを係数と考えてもいいんじゃないか。と思ったわけです。
例えば、以下の様な感じ。
> nico$cate_dummy <- 0
> nico[nico$category=="R-18",]$cate_dummy <- 0
> nico[nico$category=="VOCALOID",]$cate_dummy <- -633781.3042337
> nico[nico$category=="アイドルマスター",]$cate_dummy <- -317535.5153964
> nico[nico$category=="アニメ",]$cate_dummy <- -13644.1928142
> nico[nico$category=="エンターテイメント",]$cate_dummy <- 106135.5989756
> nico[nico$category=="ゲーム",]$cate_dummy <- 413089.5403792
> nico[nico$category=="スポーツ",]$cate_dummy <- -134995.0336501
> nico[nico$category=="その他",]$cate_dummy <- -202034.5840381
> nico[nico$category=="ニコニコインディーズ",]$cate_dummy <- -462024.0404162
> nico[nico$category=="ニコニコ技術部",]$cate_dummy <- -245200.6488111
> nico[nico$category=="ニコニコ手芸部",]$cate_dummy <- -447217.3411475
> nico[nico$category=="ニコニコ動画講座",]$cate_dummy <- -435513.2511572
> nico[nico$category=="ラジオ",]$cate_dummy <- -278794.7262665
> nico[nico$category=="演奏してみた",]$cate_dummy <- -298862.0325977
> nico[nico$category=="音楽",]$cate_dummy <- -252926.8677504
> nico[nico$category=="科学",]$cate_dummy <- -138468.1206673
> nico[nico$category=="歌ってみた",]$cate_dummy <- -153140.9438510
> nico[nico$category=="作ってみた",]$cate_dummy <- -407117.6575064
> nico[nico$category=="自然",]$cate_dummy <- -294326.5154677
> nico[nico$category=="車載動画",]$cate_dummy <- -415733.9077010
> nico[nico$category=="政治",]$cate_dummy <- -257040.9445217
> nico[nico$category=="東方",]$cate_dummy <- 74088.7571201
> nico[nico$category=="動物",]$cate_dummy <- -55178.6406359
> nico[nico$category=="日記",]$cate_dummy <- -258370.2362217
> nico[nico$category=="描いてみた",]$cate_dummy <- -413861.9118160
> nico[nico$category=="踊ってみた",]$cate_dummy <- -206639.9256112
> nico[nico$category=="旅行",]$cate_dummy <- -432103.3313191
> nico[nico$category=="料理",]$cate_dummy <- -225171.7897805
> nico[nico$category=="例のアレ",]$cate_dummy <- -198804.3473174
> nico[nico$category=="歴史",]$cate_dummy <- -382580.6157342
> nico.lm2 <- lm(view~comment+mylist+cate_dummy, data=nico)
> summary(nico.lm2)
Call:
lm(formula = view ~ comment + mylist + cate_dummy, data = nico)
Residuals:
Min 1Q Median 3Q Max
-3395324 -118156 -20216 55338 5883875
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 458064.530644 5970.408684 76.72 <0.0000000000000002 ***
comment 0.153421 0.008446 18.16 <0.0000000000000002 ***
mylist 28.047661 0.187128 149.88 <0.0000000000000002 ***
cate_dummy 1.000000 0.017673 56.58 <0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 343100 on 8996 degrees of freedom
Multiple R-squared: 0.7591, Adjusted R-squared: 0.759
F-statistic: 9449 on 3 and 8996 DF, p-value: < 0.00000000000000022
思った通り、係数は1となり、自由度調整済みも大きくなりました。もし、自由度調整済み係数をもとめられているけれども、ダミー変数化すると自由度調整済み係数が下がってしまう場合は、上記のようにして求めた自由度調整済み係数を報告すればいいかもしれませんね(自分はそうしてます)。
ということはですよ。ということは、今、上記の解析では『コメントの係数*コメント数+マイリストの係数*マイリスト数+ダミー変数の係数+切片』という式になっているわけですが、そもそも『コメントの係数*コメント数+マイリストの係数*マイリスト数+ダミー変数の係数』の部分を一つの変数と考えたらいいんじゃね? と。そしたら、変数の数は1つだけになり、自由度調整済み決定係数の値も大きくなるはず。
やってみましょう。
> nico$allvar <- 0.153421*nico$comment + 28.047661*nico$mylist + nico$cate_dummy
> summary(lm(view~allvar, data=nico))
Call:
lm(formula = view ~ allvar, data = nico)
Residuals:
Min 1Q Median 3Q Max
-3395324 -118156 -20216 55338 5883873
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 458064.519735 3658.448760 125.2 <0.0000000000000002 ***
allvar 1.000000 0.005939 168.4 <0.0000000000000002 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 343100 on 8998 degrees of freedom
Multiple R-squared: 0.7591, Adjusted R-squared: 0.7591
F-statistic: 2.835e+04 on 1 and 8998 DF, p-value: < 0.00000000000000022
はい。確かに自由度調整済み決定係数が大きくなり、表示の上では決定係数と同じになりました(計算してみたら分かりますが、全く同じではありません。決定係数よりは小さくなります)。
自由度調整済み決定係数は違いますが、上記3つ(決定係数が0.7591となってる解析)は、どれも同じ予測値を算出します。だからといって参考にならないかというとそういうわけではないのですが、あまりアテにするのもよくないような気がします。少なくとも、サンプル数がかなり多ければ(別にどれぐらいの数以上かを想定してるわけではないです)、決定係数だけを見てもいいんじゃないかと。まあ、変数を一つ増やすか増やさないかの参考なら使えるかもしれませんが。
最後にもう一度言っておきますが、自分は統計学を勉強して1ヶ月程度しかたってない初心者の中の初心者です。もしかしたら盛大な勘違いをしているかもしれません。もし、おかしなことを書いてるなら指摘してください。

コメント